二値分類モデルの評価指標　

二値分類をしたモデルを評価する場合には、そのモデルの目的によって様々な評価指標が用いられます。

評価指標

混同行列 (confusion matrix)

二値分類の学習結果を評価する場合、基本となるのは以下の４つの値です。

• 真陽性　TP　　
• 真陰性　TN
• 偽陽性　FP
• 偽陰性　FN

Pは、予測値がポジティブ、Nは予測値がネガティブ。

Tは、予測が正しい（True)の場合、　Fは、予測が間違っている（False)場合

二値分類の結果は、T/F、P/Nの組み合わせとなります。例えば、予測値がネガティブで予測が正しい場合が、TNとなります。

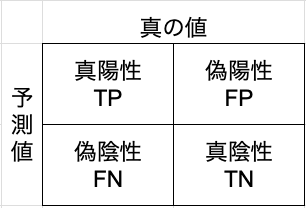
そして、これらをマトリックスで表したものが、混同行列となります。

二値分類のモデルの評価値は、この４つの値で表現できます。

正答率(accuracy)と誤答率(error rate)

正答率は正答（T)の割合で、誤答率は誤答（F)の割合なので、式で表すと以下のようになります。

$$accuracy = \frac{TP + TN}{ TP + TN + FP + FN}$$

$$error_rate = 1 - accuracy$$

accuracyをconfusion matrixで表すと以下のようになります。

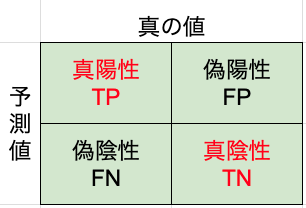
色付きの部分が分母で赤字が分子です。

正答率は、直感的にわかりやすい値ですが、実際のデータ分析ではあまり使われません。極端な例を言えば1％しかネガティブデータがない状況の場合、全てをポジティブと予測すれば99%の正答率となってしまい、意味がありません。（本当は、その1％を見つけ出したいのです。）

適合率(percision)と再現率(recall)

Precision（適合率）は、モデルが正例と予測したサンプルの中で、実際に正例であるものの割合を示します。適合率は、モデルがポジティブと予測する際にどれだけ正確であるかを示す指標です。

$${Precision} = \frac{TP}{TP+FP}$$

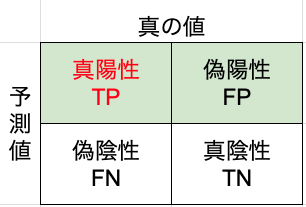
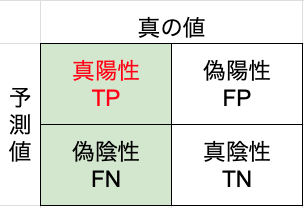
Recall（再現率）は、実際に正例であるサンプルの中で、モデルが正例と予測できた割合を示します。再現率は、モデルがどれだけ実際の正例を見逃さないかを示す指標です。

$${Recall} = \frac{TP}{TP + FN}$$

F1-score Fβ-score

PrecisionとRecallとは、トレードオフの関係にあります。これらの値のバランスを取るために調和平均を計算した結果がF1-scoreになります。

調和平均 H は、 n 個の数値 、x1​,x2​,…,xn​ の逆数の算術平均の逆数として定義されます。具体的には、次のように表されます

$$H = \frac{n}{\frac{1}{ x_1} + \frac{1}{ x_2} + ... +\frac{1}{ x_n} }$$

この式に当てはめると、PrecisionとRecallの調和平均は、以下のようになります。

$${F1-score} = \frac{2}{\frac{1}{recall} + \frac{1}{precision} } = \frac{2TP}{2TP + FP + FN}$$

さらに、Fβscoreは、Recallに重みをつけた平均になります。

f1 score fβ scoreはsklearnのライブラリとして提供されており、実際のコードでは以下のように計算されます。

from sklearn.metrics import confusion_matrix, precision_score, recall_score, f1_score, fbeta_score

# 例として、モデルの予測結果と正解ラベルを用意
y_true = [1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1]
y_pred = [1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0]

# 混同行列の計算
conf_matrix = confusion_matrix(y_true, y_pred)

# 混同行列の表示
print("Confusion Matrix:")
print(conf_matrix)

# 適合率、再現率、F1スコアの計算
precision = precision_score(y_true, y_pred)
recall = recall_score(y_true, y_pred)
f1 = f1_score(y_true, y_pred)

print(f"\nPrecision: {precision:.5f}")
print(f"Recall: {recall:.5f}")
print(f"F1 Score: {f1:.5f}")

# Fβスコアの計算（例としてβ=5を使用）
beta = 5
fbeta = fbeta_score(y_true, y_pred, beta=beta)

print(f"F{beta} Score: {fbeta:.5f}")

正例の確率を予測値とする場合の評価指標

モデルによっては、1,0のラベルを出力するのではなく、ラベルが1になる確率を出力するものもあります。このようなモデルの評価値は、以下のような値が用いられます。

logloss

loglossは、予測確率と真の値との誤差を評価します。誤差なので小さいほど良い値です。

$$logloss=-\frac{1}{N}\sum ^{N}_{i=1}( y_{i}\log p_{i}+( 1-y_{i})\log( 1-p_{i}) ) $$

ここで、確率\(p_i\)は正例（ラベル＝１）の予測確率です。真の値が負例であった場合には、真の値の予測確率（即ち負の値の確率は(\(1-p_i)\)となります。したがって、真の値を予測している確率（正答率）を\(p'_i\)とすると、上記式は以下のようになります。

$$logloss=-\frac{1}{N}\sum ^{N}_{i=1}( \log p’_{i})$$

loglossをグラフ化するコードは以下のとおりです。

import numpy as np
import matplotlib.pyplot as plt

# サンプルデータ生成
true_label = 1  # 実際のクラスラベル
probabilities = np.linspace(0, 1, 100)  # 0から1までの確率分布

# LogLoss計算
logloss_values = - (true_label * np.log(probabilities) + (1 - true_label) * np.log(1 - probabilities))

# グラフ描画
plt.plot(probabilities, logloss_values, label='LogLoss')
plt.axvline(x=true_label, color='r', linestyle='--', label='True Probability')
plt.xlabel('Predicted Probability')
plt.ylabel('LogLoss')
plt.title('LogLoss vs Predicted Probability')
plt.legend()
plt.show()

出力結果です。

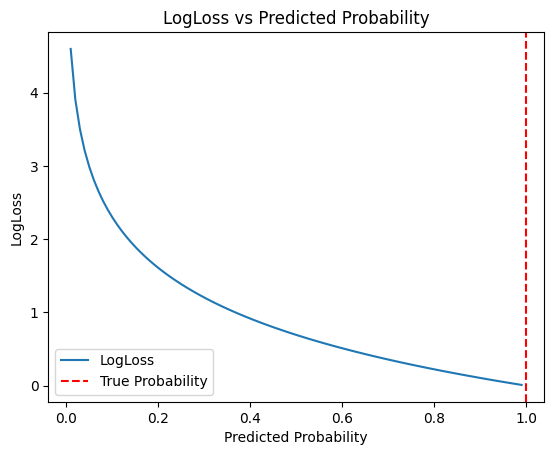
グラフを見るとわかりますが、このようにすることで、予測確率の差によって与えられるペナルティが大きく変わります。例えば、予測確率が0.9の場合には、-log(0.9)≒0.105に対して、予測確率が0.5の場合には、-log(0.5)≒0.693となり、ペナルティが大きくなります。

loglossもsklearnのライブラリとして使うことができます。

from sklearn.metrics import log_loss
import numpy as np

# サンプルデータ
y_true = np.array([0, 1, 1, 0, 1])
y_prob = np.array([0.2, 0.8, 0.6, 0.3, 0.9])

# LogLossの計算
logloss = log_loss(y_true, y_prob)
print(f"LogLoss: {logloss:.4f}")

AUC　(Area Under the ROC Curve)

AUCはその名の通り、ROC(Receiver Operating Characteristic)曲線の下の面積で定義されています。

ROC 曲線は、真陽性率（True Positive Rate, TPR）と偽陽性率（False Positive Rate, FPR）との関係を表現します。

1. 真陽性率 (True Positive Rate, TPR):
   • 真陽性率は、正例全体の中で、正例が正しく分類された割合を示します。TPRは以下の式で計算されます。
     $$ TPR=\frac{真陽性数TP}{真陽性数TP+偽陰性数FN}​$$
2. 偽陽性率 (False Positive Rate, FPR):
   • 偽陽性率は、負例全体の中で、誤って正例と予測された割合を示します。FPRは以下の式で計算されます。
     $$ FPR=\frac{偽陽性数FP}{偽陽性数FP+真陰性数TN}$$

閾値を0.0から1.0まで変化させた時の真陽性率と偽陽性率との関係を表したものがROC曲線になります。

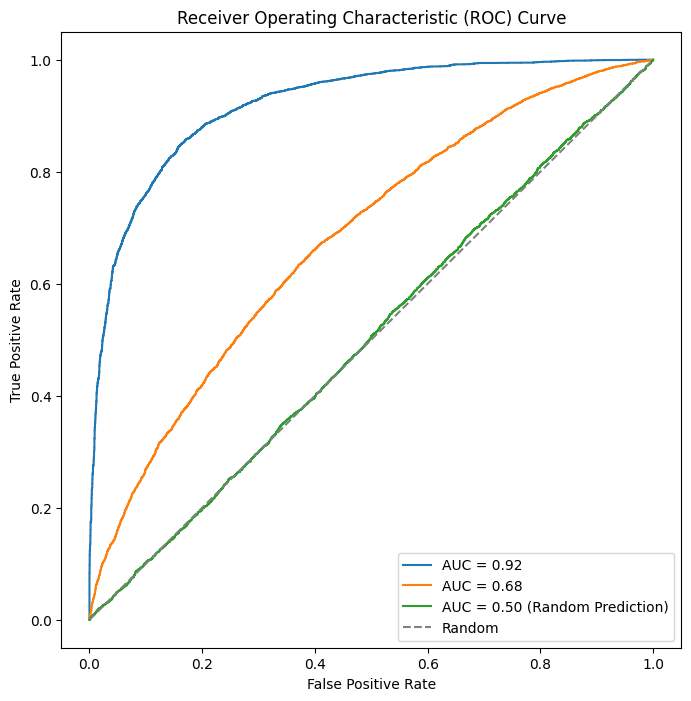
上記のグラフの例では、青い線の下の面積が一番大きく、AUC=0.92となっています。このグラフでは、TPRの増加に対して、FPRの増加が抑えられており、一番よいモデルといえます。緑の線はランダムに予測したモデルになっています。